Nanoscale SLIs

Research interests: Nanoscale solid-liquid interfaces

From the macroscopic picture to the nanoscale

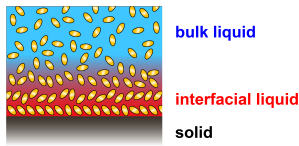
Solid-liquid interfaces are central to phenomena as disparate as protein folding and function, molecular self-assembly, corrosion, heat and charge exchanges, lubrication, wetting and crystal growth to mention only a few. Although most of these processes have obvious macroscopic consequences, they usually originate from a complex interplay of molecular-level interactions between the solid and the liquid at the interface: the liquid molecules tend to behave differently at the interface than they would in the bulk liquid due to their interaction with the surface of the solid. As a result, this so-called interfacial liquid is typically more ordered and denser than bulk liquid, and its dynamics is altered.

Cartoon representation of a solid-liquid interface. The liquid molecules (yellow) are typically more ordered and densely packed near surface of the solid. This “non bulk-like” liquid region is effectively the interface.

Wetting and the thermodynamics description

In the framework of thermodynamics, an interface between two media M1 and M2 is described by its free energy γM1,M2. The Dupré equation stated that this energy is simply the sum of both media’s surface energies minus the work of adhesion between them. In the case of a solid and a liquid (M1=S, M2=L) we have:

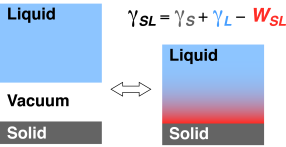
The surface energies –literally the energy per area necessary to create the surfaces by cutting through the medium considered– represents the cost induced by the dangling bonds of all the under-coordinated atoms or molecules at the newly created surface. At the interface, this energy cost can be reduced if these bonds are partially restored through interactions with the other medium. This is described by the work of adhesion which is the reversible work necessary to separate both media. The work of adhesion hence describes the affinity (or adhesion energy) between both media at equilibrium.

In the case of solid-liquid interfaces, the work of adhesion quantifies wetting. It is directly related to the contact angle formed by the liquid on the solid through the well-known Young-Dupré equation:

Note that equation shown above is a widely used approximation of the Young-Dupré equation.In the absence of chemical reactions, any restructuring of the media at the interface is driven by the work of adhesion. The work of adhesion is hence the driving force for the densification and ordering of the interfacial liquid.
Although conceptually intuitive, these thermodynamics quantities have been developed considering macroscopic (>1 μm) systems where they represent an average per surface area. When considering a system at the nanoscale, their interpretation is less obvious: even a perfect atomic plane of a single crystal will exhibit substantial lateral variations in surface energy at the atomic level. The work of adhesion can still be understood intuitively but, it makes more sense to use terms such as the local free solvation energy of the solid in the considered liquid.